Powerlifting Percentiles

Introduction
In the realm of powerlifting, the measure of an athlete’s prowess is distilled down to their total – the cumulative weight of their best squat, bench press, and deadlift. However, this raw total only scratches the surface of the competitive landscape. It’s obviously far more impressive for a 57kg/125lbs woman to lift 400kg/880lbs than it is for a 93kg/205lbs man to total the same. As a data scientist and a powerlifter, I’ve developed a tool that offers a deeper insight into how to quantify this. This tool isn’t just about numbers; it’s about context, enabling athletes to gauge their performance not just in isolation but against a broader competitive field, considering crucial factors such as bodyweight and sex.
Background
Powerlifting is a sport of nuance, where athletes compete within categories defined by bodyweight and sex to ensure fairness and equity. However, comparing performance across these categories or even within them can be complex due to the diversity of human physiques and strength capabilities. Traditional metrics like DOTS, Wilks, and IPF GL points provide a solution, but they often seem abstract — what exactly does a 400 DOTS mean? They transform performances into scores that, while useful for competition, lack intuitive meaning for many athletes and coaches.
Recognizing this gap, my aim was to create a tool that transcends traditional scoring systems, offering a percentile-based analysis of a powerlifter’s total. This approach is grounded in statistical analysis, providing a clear, intuitive understanding of where an athlete stands among their peers. For instance, knowing that a 600kg/1322lbs total at a bodyweight of 90kg/198lbs places a male athlete in the top 30% of competitors offers a more relatable sense of achievement than a score or coefficient might.
This tool is designed for powerlifters who seek a deeper understanding of their competitive standing, coaches aiming to benchmark their athletes, and enthusiasts who enjoy dissecting the analytics behind the sport. By inputting sex, bodyweight, and total lift, users receive a percentile ranking that reflects their performance in relation to a comprehensive database of powerlifting outcomes. This not only helps in setting realistic goals and strategies but also fosters a greater appreciation for the nuances of strength sports.
Give it a try here: http://powerlifting-percentiles.vercel.app
Let’s dig in
Using the publicly available powerlifting dataset from https://data.openpowerlifting.org/, we can start digging into all kinds of data about powerlifting competitions. The first thing that’s useful to look at is what the distribution of totals looks like for a given sex and bodyweight. Below are the distributions for men and women from bodyweights of 50kg/110lbs to 120kg/265lbs.
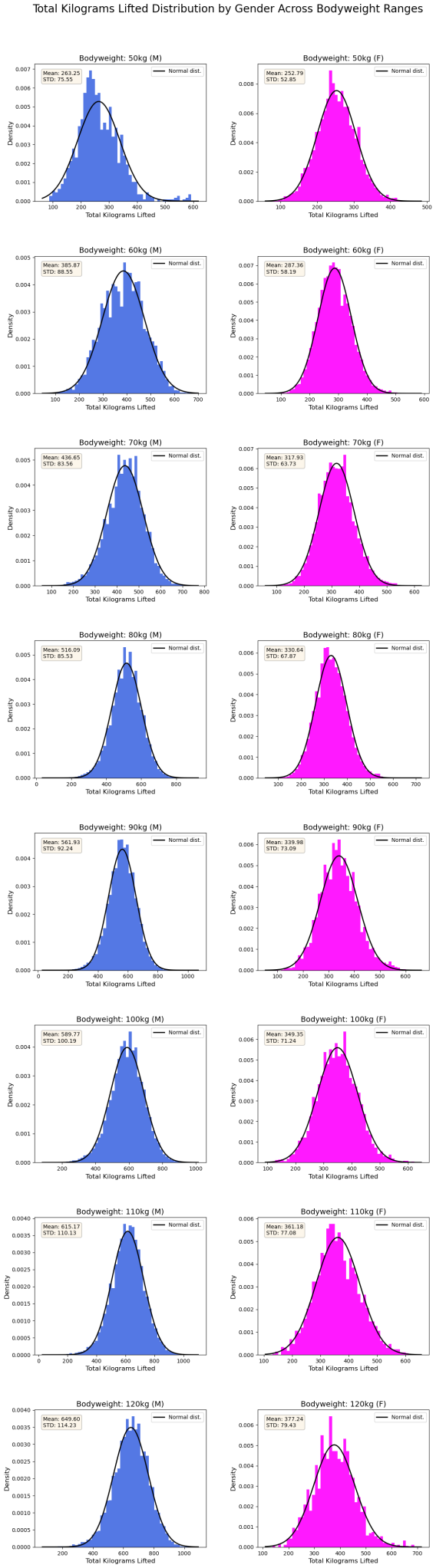
You’ll notice that a normal distribution does a really good job of modeling the distribution of totals for each of the given sex/bodyweight pairs. Going into this, I was expecting there to be longer tails, especially on the right side because I am not filtering out non-tested competitions. Nevertheless, the normal distribution does a great job. It’s always cool when numbers just work like that.
We already have everything we need to calculate the percentiles for different totals — we’d just need to compute the mean and standard deviation for every bodyweight in the dataset, which is totally doable since the dataset has plenty of data on a wide range of body weights. We could simply look at each kilogram of bodyweight from 40kg up to 200kg, and compute the mean and standard deviation for males and females. This would give us (160 unique bodyweights) * (2 sexes) * (2 parameters) = 640 numbers.
However, this sucks and is ugly. The beauty of statistics is that you can take many numbers and model them using few numbers. So let’s keep going.
What would be nice at this point is a way to predict the mean and standard deviation based on sex and bodyweight. Let’s see if we can do that. I’ll start by plotting the mean and standard deviation for males and females based on bodyweight.
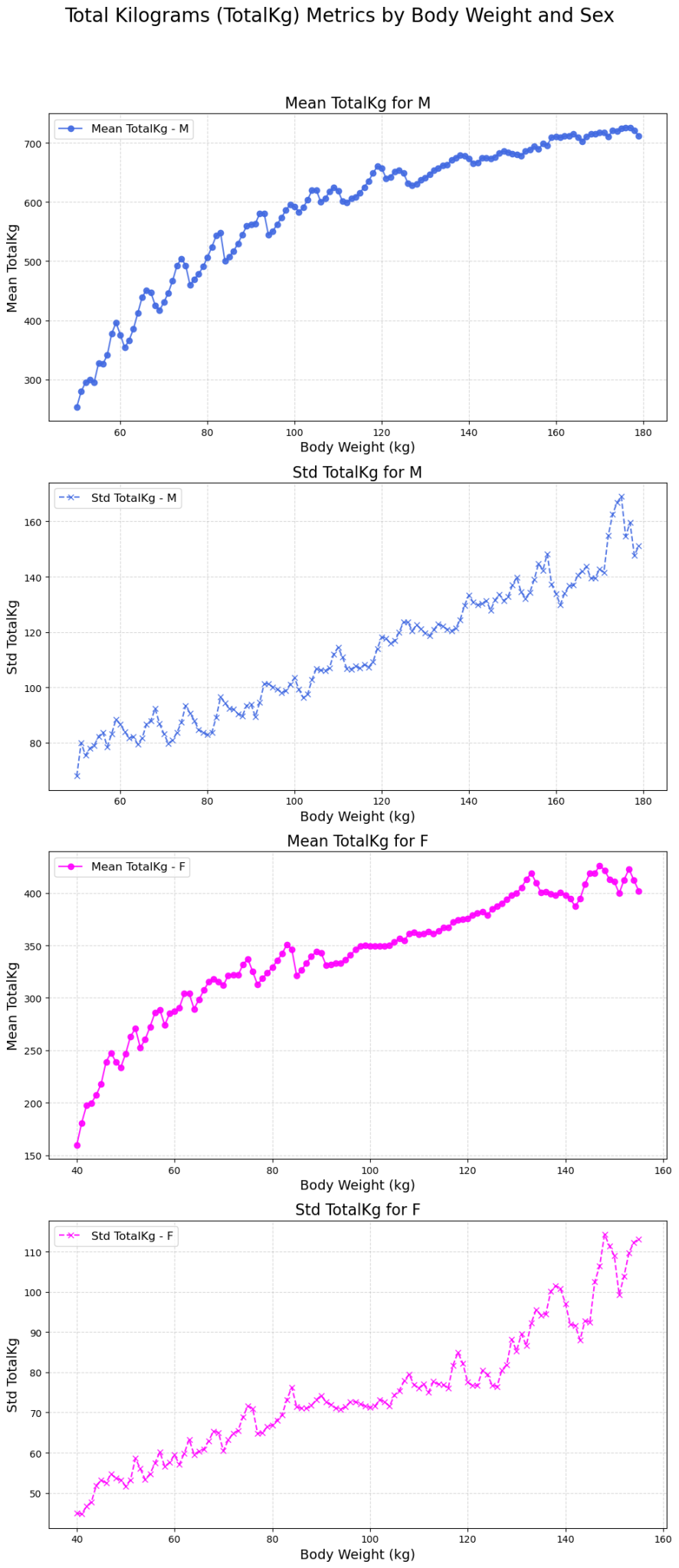
We can work with this. The plots for the mean looks to be logarithmic. This would make sense, as relative strength tends to decrease at higher and higher bodyweight. Let’s see if we can fit a curve of the type f(x) = a * ln(b * X + c) to these data points.
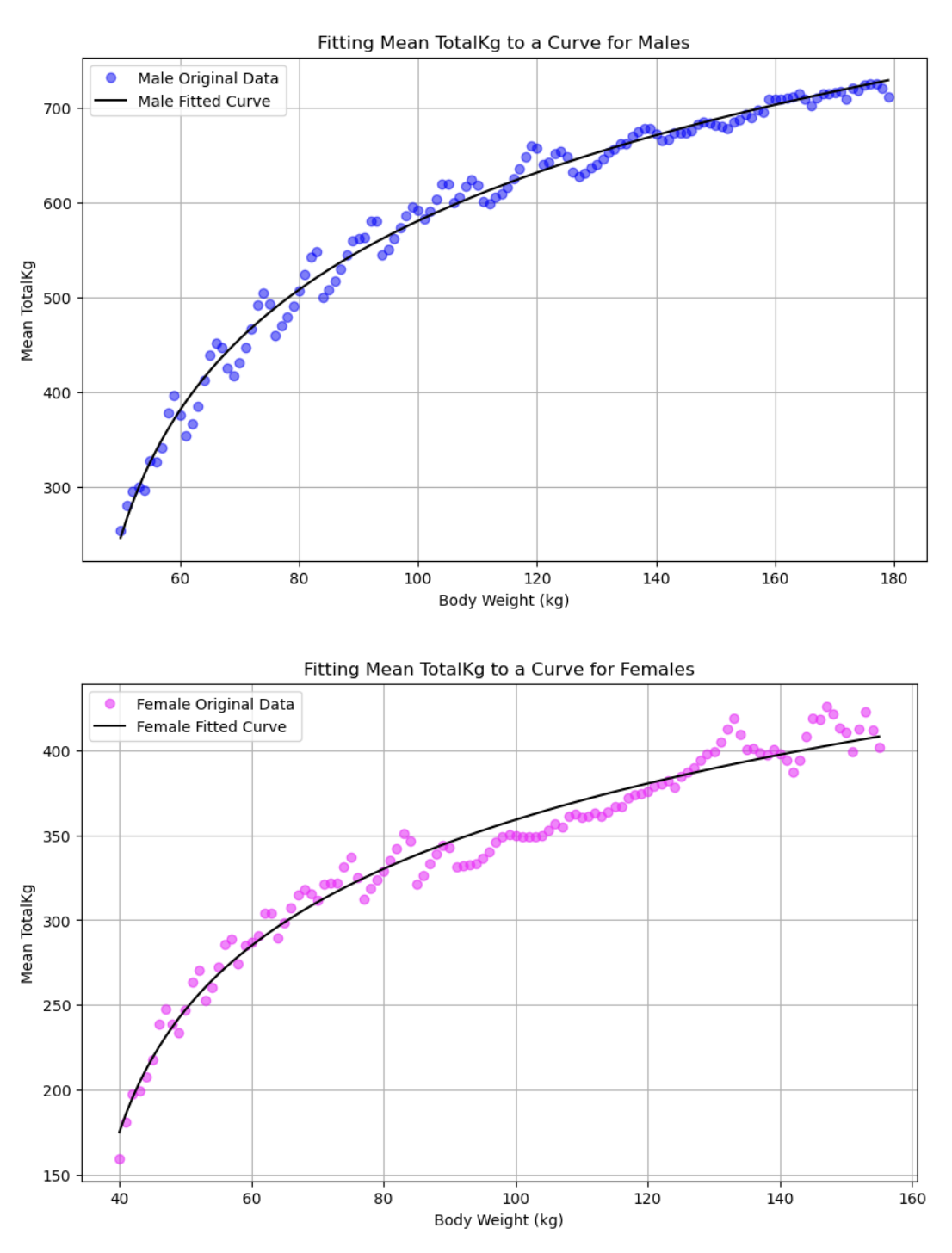
That’s looking really good! Now, let’s do something similarly with the standard deviations. The standard deviations tend to increase with respect to bodyweight, but it doesn’t look linear. There’s a slight bend in it making it get bigger more rapidly at higher body weights. Let’s try fitting a polynomial function of degree 3 to the data.
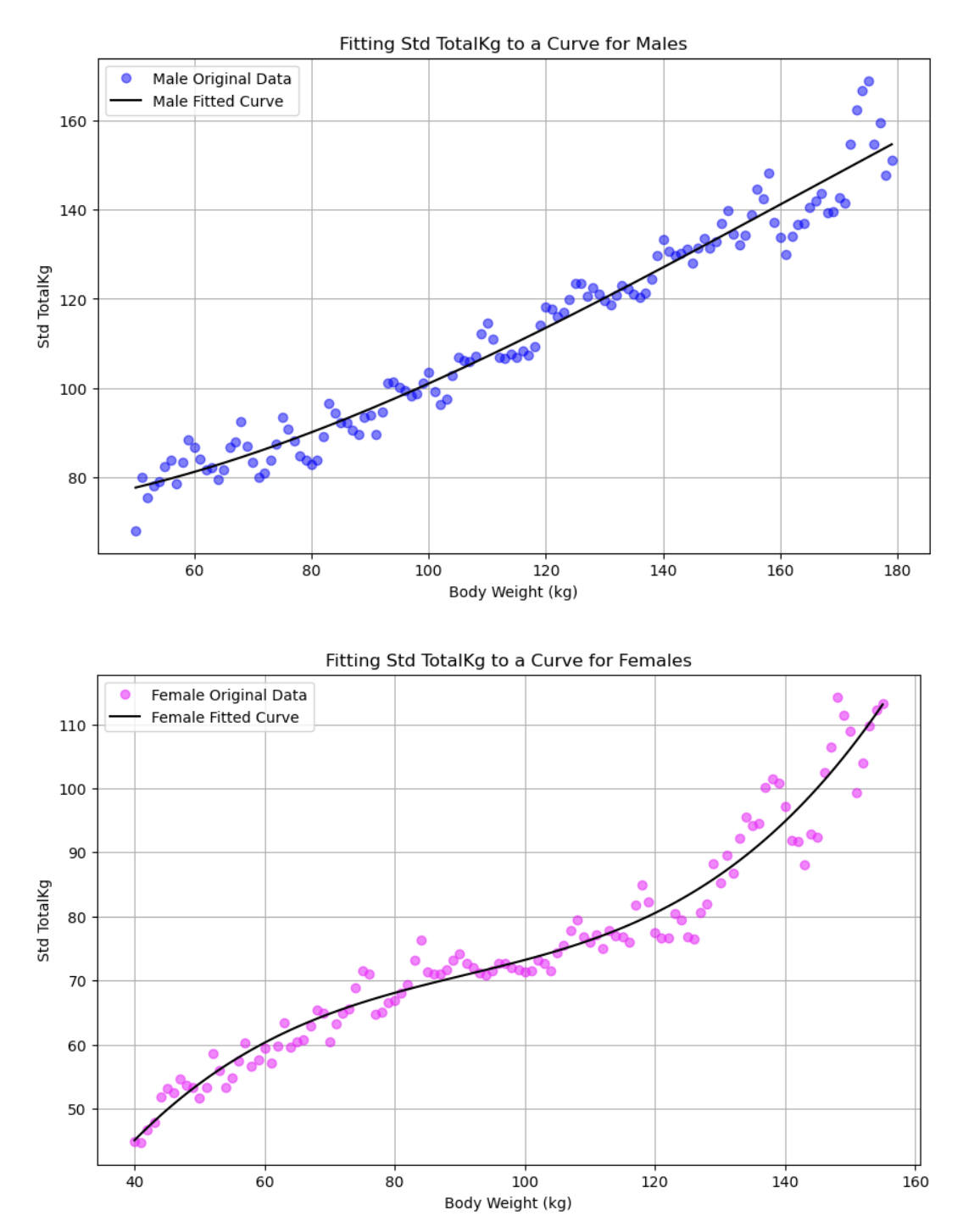
That’s pretty good! Now, for each sex, we have just 3 numbers to calculate the mean, and 4 to calculate the standard deviation, giving us 14 total. That’s far fewer than the 640 from before and has the added benefit of smoothing out the data for us.
Piecing it all together
Now that we have a model for the mean and standard deviation based on bodyweight, we can answer our original question of calculating the percentile a given total is based on bodyweight and sex. Here’s how you’d do it in Python:
import numpy as np
from scipy.stats import norm
def mean_curve_func(x, A, B, C):
return A * np.log(B * x + C)
def std_curve_func(x, A, B, C, D):
return A + B * x + C * x ** 2 + D * x ** 3
def calculate_percentile(total, bodyweight, sex):
if sex == 'M':
a_mean, b_mean, c_mean, a_std, b_std, c_std, d_std = (172.60089846052378, 0.4968538227117669, -20.750205863276193, 72.0417687388453, -0.09976586871208123, 0.004811979334739356, -9.2217747522473e-06)
elif sex == 'F':
a_mean, b_mean, c_mean, a_std, b_std, c_std, d_std = (82.83876086730504, 1.1234655444197217, -36.36091255869513, -29.441592676328575, 2.822549893189308, -0.028338224120590404, 0.00010359303020098536)
else:
return (calculate_percentile(total, bodyweight, 'M') + calculate_percentile(total, bodyweight, 'F')) / 2
mean = mean_curve_func(bodyweight, a_mean, b_mean, c_mean)
std = std_curve_func(bodyweight, a_std, b_std, c_std, d_std)
cdf_value = norm.cdf(total, loc=mean, scale=std)
percentile_score = cdf_value * 100
return percentile_score
Note: The values you see above are based on male body weights between 50kg and 180kg, and female body weights between 40kg and 156kg. This is where most of the data is. Beyond those numbers, the predictions might get weird.
How does this compare to DOTS, Wilks, and IPF GL points?
DOTS, Wilks, and IPF GL points are all calculated by multiplying the total by some coefficient. For DOTS and Wilks, these coefficients are inverse polynomials (k / (a + bbodyweight^1 + cbodyweight^2 + …)). For IPF GL, the coefficient is calculated using an exponential (k / (a – (b * np.exp(-c * bodyweight)))).The exact parameters were determined statistically for each method.
Looking at how they all compare, we can see they all correlate with each other. The notable thing here is that IPF GL points correlate the least with the other methods.
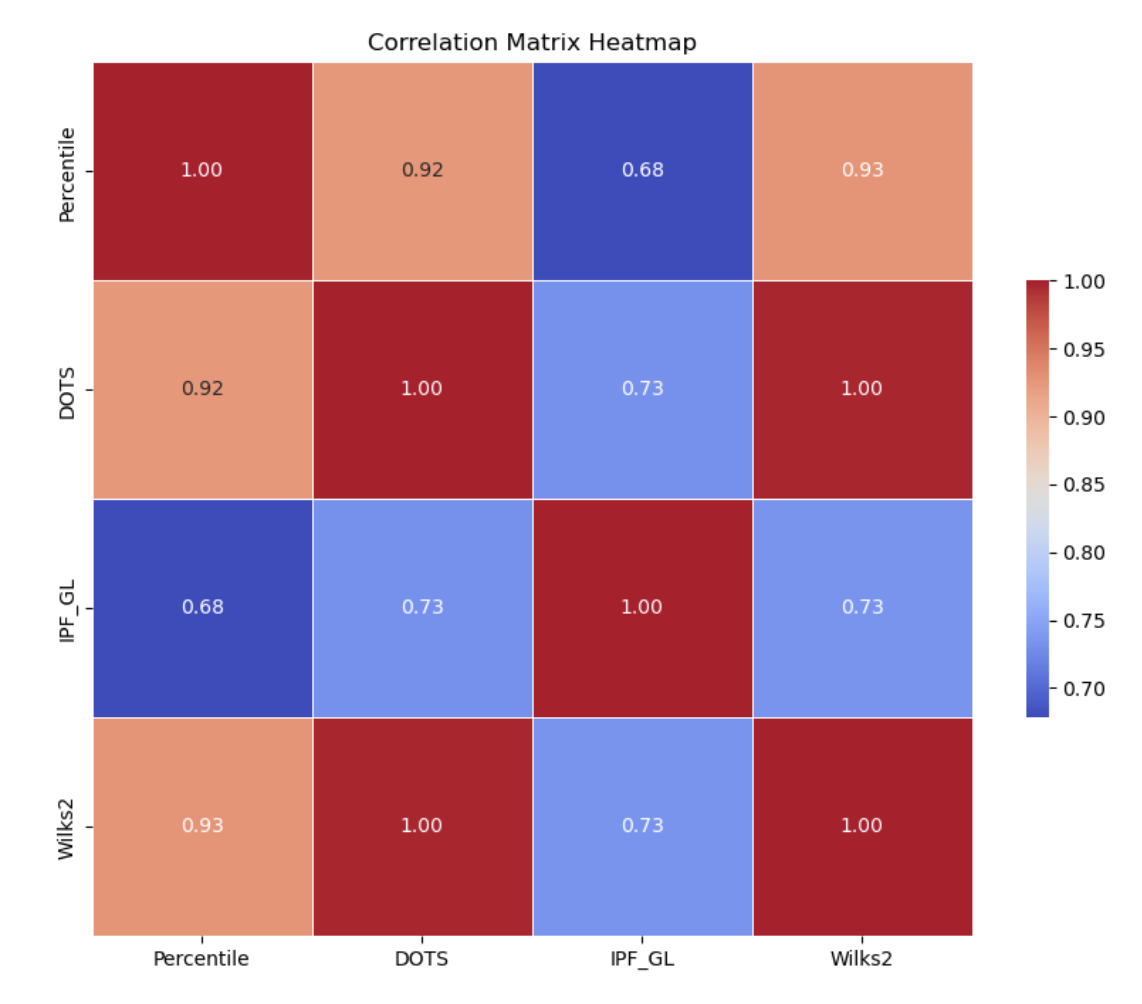
To get a sense of what this means for athletes, here are the top athletes on Open Powerlifting according to this percentile method, along with their DOTS, Wilks, and IPF GL scores.
| Name | Sex | TotalKg | BodyweightKg | Percentile | DOTS | IPF_GL | Wilks2 |
| Kristy Hawkins | F | 687.5 | 73.6 | 99.99999889 | 676.3649699 | 137.6691834 | 807.3500652 |
| Samantha Rice | F | 702.5 | 84.45 | 99.99999352 | 644.7747172 | 132.3909801 | 778.6499139 |
| Chakera Ingram | F | 692.5 | 81.5 | 99.99999292 | 646.5530622 | 132.37712 | 777.9553236 |
| Marianna Gasparyan | F | 580 | 57.7 | 99.99998561 | 659.2404949 | 134.8196479 | 785.5358158 |
| John Haack | M | 1022.5 | 89.9 | 99.99996847 | 661.5198215 | 136.0079451 | 784.704424 |
| Hunter Henderson #1 | F | 670 | 81.4 | 99.99996068 | 625.9219259 | 128.1412635 | 753.0418489 |
| Agata Sitko | F | 600 | 68.9 | 99.99971785 | 612.1988041 | 124.4045128 | 728.5908302 |
| Amanda Lawrence #1 | F | 647 | 83.51 | 99.99968344 | 597.0001089 | 122.4662853 | 720.0980709 |
| Sarah Lewis #1 | F | 597.5 | 68.7 | 99.99968057 | 610.6562174 | 124.0875774 | 726.69048 |
| Stefanie Cohen | F | 525 | 54.8 | 99.99967016 | 617.3928361 | 126.947125 | 737.7863221 |
| Prescillia Bavoil | F | 585 | 66.46 | 99.99959918 | 609.421842 | 123.8323692 | 724.672949 |
| Brianny Terry | F | 620 | 75.8 | 99.99959039 | 600.5065677 | 122.3891255 | 718.1649633 |
| Carola Garra | F | 582.5 | 67.17 | 99.99940009 | 603.0764455 | 122.5373256 | 717.2647958 |
| Blake Lehew | M | 915 | 82.3 | 99.99930696 | 620.6683121 | 127.2039382 | 737.0959947 |
| Jawon Garrison | M | 915.5 | 82.5 | 99.99927919 | 620.1529464 | 127.1172106 | 736.4631197 |
| Karlina Tongotea | F | 610.5 | 75.6 | 99.99924652 | 592.1243591 | 120.6649126 | 708.0097076 |
| Ashley Contorno | F | 600 | 73 | 99.99915438 | 592.8923493 | 120.6423087 | 707.3821176 |
| April Mathis | F | 705.34 | 113.4 | 99.99911051 | 575.6468577 | 122.169002 | 720.5754021 |
| Kiersten Scurlock | F | 677.5 | 102.8 | 99.99904305 | 572.0828223 | 119.960434 | 708.0951469 |
| Susan Salazar | F | 540.5 | 60 | 99.998912 | 599.1689101 | 122.1746983 | 712.9371962 |
| Austin Perkins #1 | M | 851 | 74.24 | 99.99890943 | 614.5368092 | 124.7255278 | 730.2852624 |
| Andrzej Stanaszek | M | 600 | 51.3 | 99.99883793 | 582.152431 | 107.0338839 | 676.3199621 |
| Jade Jacob | F | 519.5 | 56.57 | 99.99876659 | 598.1520425 | 122.5546881 | 713.4353175 |
| K’Aunica Byrd | F | 567.5 | 66.3 | 99.99866166 | 592.0254095 | 120.2996737 | 703.9607689 |
| Natalie Richards #1 | F | 516.5 | 56.36 | 99.99859279 | 596.1558462 | 122.1920582 | 711.197074 |
| Jamal Browner | M | 1052.5 | 109.4 | 99.99854768 | 624.650732 | 127.5091682 | 740.2865278 |
| Taylor Atwood | M | 838.5 | 73.63 | 99.99836106 | 608.7664483 | 123.4208063 | 723.4173207 |
| Yelena Espinoza | F | 507.5 | 55.4 | 99.99821838 | 592.4788791 | 121.6665083 | 707.5192574 |
| Alana Hynes D’Aquino | F | 567.5 | 67.4 | 99.99816496 | 586.385427 | 119.1455463 | 697.4635609 |
| Barbara Lee #1 | F | 567.5 | 67.4 | 99.99816496 | 586.385427 | 119.1455463 | 697.4635609 |
| Stacy Burr | F | 565 | 66.9 | 99.99810812 | 586.3274069 | 119.1354545 | 697.2898861 |
| Sherine Marcelle | F | 633.5 | 89.2 | 99.99801303 | 567.0205375 | 117.0183273 | 689.085185 |
| Evie Corrigan | F | 481 | 51.85 | 99.99779858 | 587.4710361 | 121.7581506 | 705.0633366 |
| Brittany Bowles | F | 527.5 | 59.75 | 99.99746032 | 586.3029417 | 119.5833862 | 697.7130429 |
| Jessica Springer | F | 687.5 | 113.9 | 99.99736365 | 560.304642 | 118.9762188 | 701.6626694 |
| Meghan Scanlon | F | 542.5 | 63 | 99.99726528 | 583.4668646 | 118.6898673 | 693.6525644 |
| Tess Heaslip | F | 587.5 | 74.7 | 99.99716877 | 573.4269642 | 116.7890919 | 685.1031833 |
| Alisha Luna | F | 475 | 51.5 | 99.99711682 | 582.8913148 | 120.9462342 | 699.9967763 |
| Daniella Melo | F | 613 | 83.55 | 99.99709663 | 565.4983105 | 116.008709 | 682.1349969 |
| Jenn Rotsinger | F | 465 | 50.2 | 99.99705247 | 580.9970924 | 121.1121833 | 699.4596024 |
| Andrea Armstrong | F | 510 | 57.1 | 99.99686027 | 583.6353396 | 119.4715278 | 695.7884537 |
| Viktoriya Ilieva | F | 592.5 | 77.5 | 99.99640777 | 567.3140859 | 115.7633975 | 679.5936319 |
| Jessica Buettner | F | 585 | 75.25 | 99.99628754 | 568.7775928 | 115.8812638 | 679.8777718 |
| Chad Penson | M | 925 | 90 | 99.99612693 | 598.1057663 | 122.9715227 | 709.4713579 |
| Jesse Norris | M | 922.5 | 89.72 | 99.99597167 | 597.4278642 | 122.8278584 | 708.6963879 |
| Chloe Lansing | F | 555 | 67.3 | 99.99588536 | 573.962045 | 116.6213647 | 682.66511 |
| Allison Hind | F | 580.6 | 74.57 | 99.995734 | 567.2162148 | 115.5152526 | 677.607025 |
| Tiffany Chapon | F | 431.5 | 46.77 | 99.99566294 | 567.5658408 | 120.1975943 | 688.9587868 |
| Amanda Smith #5 | F | 575 | 73 | 99.99562297 | 568.1885014 | 115.6155458 | 677.9078627 |
| Terri Ashley | F | 595 | 79.5 | 99.99557729 | 562.3969365 | 114.9435291 | 675.1403831 |
Conclusion
Wrapping up, the development of this percentile calculator for powerlifters is a straightforward step towards making sense of how totals stack up across different weight classes and sexes. It’s a practical tool that helps athletes, coaches, and enthusiasts get a quick glimpse into where a lifter’s performance sits on the broader spectrum without diving into complex formulas or coefficients.
Unlike traditional metrics like DOTS, Wilks, and IPF GL points, which serve their purpose in scoring and standardizing competition performances, this tool offers a simpler, more intuitive way to understand one’s standing. By translating totals into percentiles, it directly connects an athlete’s efforts to a position within a defined peer group, making the numbers more relatable and understandable.
In conclusion, this percentile calculator is a modest contribution aimed at making data a bit more accessible and meaningful for the powerlifting community. Whether you’re comparing your progress, setting new targets, or just satisfying your curiosity about where you stand, it’s here to provide those insights in a simple and straightforward manner.
PS, all the code for these calculations is available on GitHub here: https://github.com/prestoj/powerlifting-percentiles-analysis